Socratic Seminar- Who is the goat?

Over the last 3 weeks in my Humanities class called Forbidden Books, we have been studying about
Socrates and his struggles. Socrates was a classical Greek philosopher that is credited as one of the founders of Western philosophy, He basically went against societies norms and questioned everything. He questioned their Gods, leaders, and also who is actually smart. Basically in this Action Project we were given a option to pick any topic to create a Socratic seminar about. We had to give facts, important details, and make sure in the end someones opinion changed. My group decided to make one based on who is the Greatest of all time NBA player. Anyway heres our video enjoy.

From this project I have learned how to communicate effectively with my classmates and create a conversation while providing evidence to back up what I say. I have learned to question the unquestionable and question the things that people wouldn't dare to. Its OK to be different and think different, all things sometimes are meant to be changed.

Pascals Triangle

Over the course of Prove It or Lose It for the term we have went over a lot of things. Went went over topics like combinations, permutations, Pascal's Triangle and how to determine how many routes to get from one place to another. This lead to making an online poster and some even graphed theirs. In prove it or Lose it we have also learned about some history of math, and we also watched an informational video. To me what was really fun was that I got to work with my classmates and problem solve through some activities. We would debate and brainstorm about one problem for the whole class period until someone could prove how they got there answer. This was unique and interesting.

Combinations

A combination is a sequence in numbers which order doesn't matter. They could be posted as a selection or a lottery.

Example word problem: Nakiyah has 7 songs to pick from and will play 3. How many different ways can he perform each song 7C3=

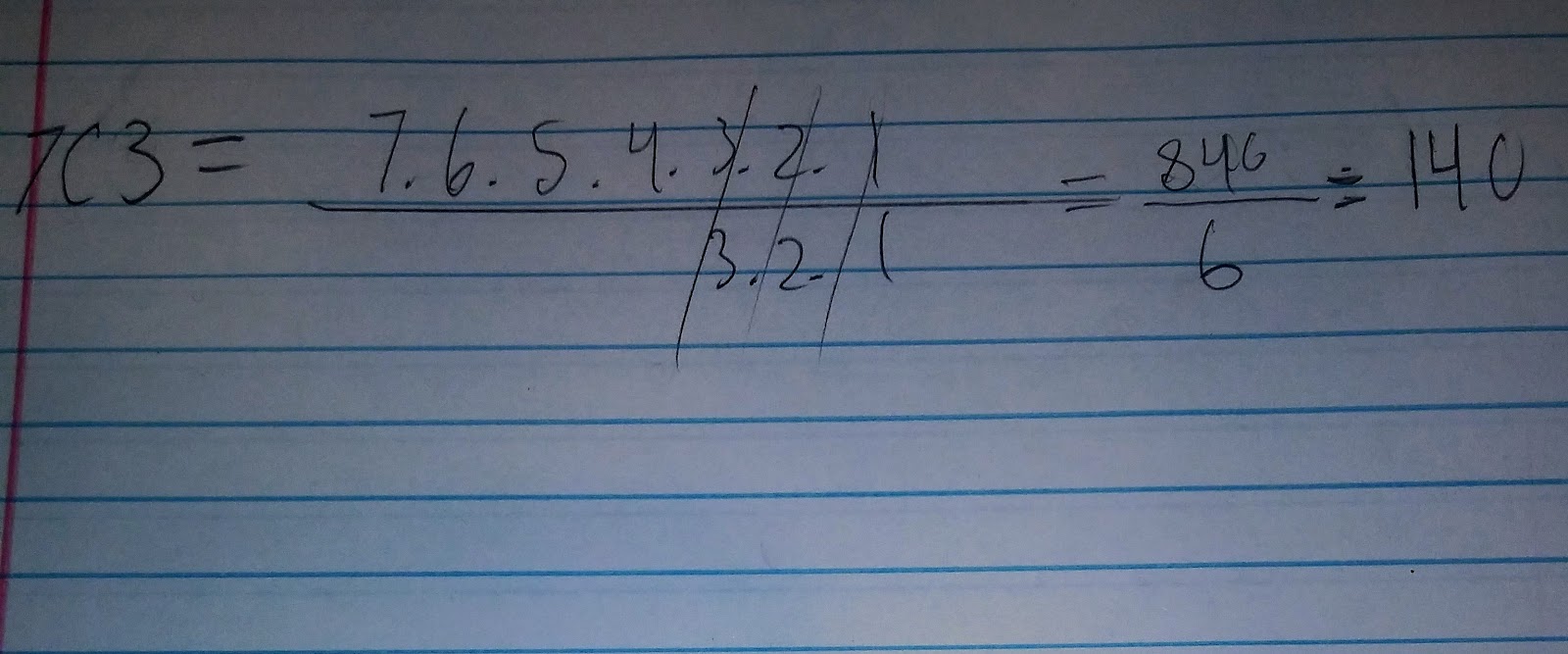J.L  Combination Example. (2018)
  

What is a Pascals Triangle

In mathematics, Pascal's triangle is a form of the binomial coefficients. It is named after the French mathematician Blase Pascal, although other mathematicians studied it centuries before him in India, Persia, China, Germany, and Italy.

A unique mathematical pattern within Pascal’s triangle

The diagonals going along the left and right edges contain only 1's.

Another observation that I made was that in the two triangles above the second one adds up to get the one below it. (example) 4 and 3 in the top and that would mean 7 in the one below it

J.L  Example of Unique Pattern. (2018)

Create an artistic representation of Pascal’s Triangle.

Example of Pascals Triangle. (2018)

Pascals Triangle (Wills Copy)

J.L Drawing of Pascals Triangle. (2018)

My Pascal's Triangle (J.L)

For my Pascal's Triangle representation I choose to create a triangle depicting a smiley face on it.
On the sides I noticed that there are all ones, and this was interesting for me. In this image I am conveying that my combination problem relates to my triangle. If you go down 7 and over 3 you'll find the answer 140 .My triangle although does not have equal proportions in each side but thats why I did it. I wanted it to be different by adding extra triangles and bigger triangles. Pascal's Triangles portions are the same, and so is the numbers on each side. But I also noticed that in both are triangles we had smaller triangles also.

Here's what I mean

(J.L)

From this project I have learned about combinations and Pascal's Triangle. The process for me trying to understand what we were trying to do was kinda challenging. The thing that was rewarding was that I learned something new and had fun doing it. But if I was to take Prove it or lose it aging I would like a better explaining of the project, and be able to get more help.

Basketball Court Reflection

Over the past three weeks in my workshop Prove it or Lose it we have been discussing many proofs and the why as to just solving a problem. This course was very interesting and focused mainly on how to understand a problem in depth. Recently we have went over reflections in the real world and how to incorporate them in class. We played a game called Pong and this showed us an example of a real life reflection. To me this was pretty neat and I saw that I could them make a reflection with angles on my own topic. So the thing that I would want to make a reflection of is a basketball court. This will be a difficult task but I think I could do it.

What are reflections?

A reflection is a transformation in which the figure is the mirror image of the
other. Basically this means something depicted on the other side of a figure
and is reflecting. Reflection can also be called as flip.

Find a reflection based on a real life = Basketball Court

Here I made a reflection of this court on a graph going by ten. I decided to place the dots at the foul line on each court.

Coordinates

Reflected on its X axis.(-3,8.75) (-6,8.75)

(5,8.85) (3, 8.75)
I did this on GeoGebra that's how I got the x y coordinates.

For my second measurement I came to the conclusion to make an angle on the two separate court

On the left

• Acute Angle from both free throws to baseline of half court 35/40 

On the right

• Right angle from the top of the key to the free throw to the corner baseline 90 

In conclusion from this action project I have learned how to identify slope on a graph from different viewpoints and variations. I have learned some new math vocabulary words and how to problem solve. Overall this project was very frustrating and unclear on certain expectations. Also I couldn't get GeoGebra to corporate what I was thinking so my pictures were done by hand but the coordinates for the graph were from GeoGebra. Next time I will do my best to work harder and more persistent.